MIM制模与模拟（11.1-11.2）

目录

• 11.1 混合过程的制模和模拟

• 11.1.1 制模

• 11.1.2 数值方法

• 11.1.3 应用

• 11.2 注塑成型过程的建模与模拟

• 11.2.1 理论背景和控制方程

• 11.2.2 数值模拟

• 11.2.3 实验材料特性和验证

11.1 混合过程的制模和模拟

在分析与粉末注射成型（PIM）相关的混合过程时，我们主要关注无分子扩散的分布混合，这取决于给定材料特性和操作条件下特定混合器几何形状的流动运动学。这是具有无限Peclet数的流的情况。可以使用有限元法（FEM）解决该混合器中的流动问题。对于PIM过程等流体-颗粒相互作用运动学的混合分析，可以采用颗粒跟踪方法。在下通道位置的颗粒分布用于定性和定量表征混合过程。基于粒子分布的混合度量，称为信息熵，可以用来量化混合程度。

11.1.1 制模

假设要混合的材料是均匀的广义牛顿流体，流动仅由粘性力控制，忽略惯性力，这是高粘性PIM原料混合分析中的合理假设。在蠕动流动状态下，连续性和动量平衡方程如下：

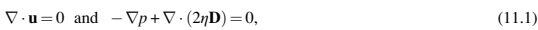
h是粘度，D是变形张量的速率，p是压力，u是速度。原料的粘度通常由剪切速率γ、温度T和压力p的函数表示。Cross Williams Ladel Ferry（WLF）模型是PIM中原料的粘度模型之一，定义如下：

h0是WLF模型描述的零剪切速率粘度，由

A2¼Ae2+D3p和T*¼D2+D3p以及材料参数A1、A2、D1、D2和D3通过使用实验粘度数据的曲线拟合确定。尽管PIM原料具有更复杂的流变响应，但校正并不显著。

11.1.2 数值方法

有限元公式

为了获得速度场和压力分布，使用Galerkin有限元法求解方程组（11.1）以及适当的边界条件。不可压缩Stokes方程的弱公式由下式给出

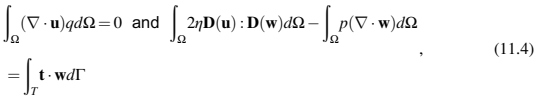
W是计算域，G是边界，W是速度u的加权函数，q是压力p的加权函数

在三维（3D）流动模拟中，数值积分后得到的矩阵方程是一个巨大的稀疏对称矩阵。因此，需要一种有效的方法来求解所得的矩阵方程。并行直接求解器，如PARDISO（Schenk&G€artner，2004），可用于在具有多个CPU的并行计算机上求解生成的稀疏矩阵。

粒子追踪方法

基于粒子跟踪方案的混合分析包括三个步骤：

1. 流动分析以获得混合装置的速度场；

2. 粒子跟踪步骤，以获得混合器末端的粒子分布；

3. 从获得的颗粒分布定量混合。

要跟踪粒子的位置，需要解决的问题是一个常微分方程

x是粒子位置矢量，u是粒子速度，t是时间。四阶龙格-库塔方法被广泛用于积分常微分方程组，方程（11.6），关于时间。然而，在某些情况下，可以简化问题，从而可以解决2D问题而不是3D问题。通过改变原始方程，可以减小系统的尺寸，并且可以使用沿下通道方向的固定空间增量来执行积分。这种方法具有几个优点，例如更快的解决方案，并且易于根据下通道方向表示任何横截面区域的动力学。该方案仅限于速度场的所有轴向分量在整个域中均为正的问题，即无回流。由此产生的2D问题表示如下：

其中u、v和w分别表示沿x、y和z坐标的速度分量。因此，粒子沿着轴向位置而不是时间进行跟踪。

11.1.3 应用

混合器和混合材料

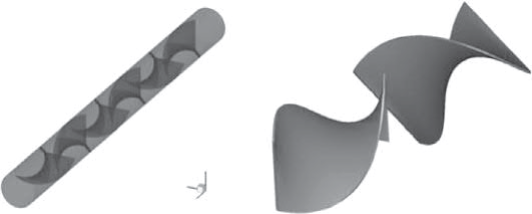
静态混合器，称为Kenics混合器，作为PIM原料制备的混合装置，在斯托克斯流动状态下运行，惯性可忽略不计。图11.1描绘了六元件静态混合器的代表性几何结构（图11.1A），其中混合元件在交替方向上扭曲180度（图11.1B），用于模拟。

羰基铁的PIM原料在63vol%固体负载下的粘度通过毛细管流变仪测量，遵循ASTM 3835-96，针对三个温度和一系列剪切速率。根据这些数据，我们通过曲线拟合确定了Cross-WLF模型的七个系数：n¼0.4999、τ*¼0.0005734 Pa、D1¼1.50 1011Pa s、D2¼373.15 K、D3¼0 K/Pa、A1¼6.30 K和Ae2¼51:6K。

 (A)                                                          (B)

图 11.1 Kenics静态混合器。（A） 带有六个螺旋元素的混合器的阴影图像。（B） 两个在交替方向上扭转180度的混合元件称为LR-180元件。

基于流动特性的Kenics混合器工作原理

首先，使用有限元法求解流动问题。混合器几何结构被划分为具有519155个节点的344510个十节点四面体单元。速度的二次插值和压力的线性插值均满足速度和压力插值函数的相容条件。Kenics混合器的混合原理也基于面包师的变换，包括重复拉伸、切割、堆叠，这是在管道流中实现的，叶片在交替方向上以固定角度扭曲。图11.2显示了前半个周期的混合过程，叶片逆时针旋转180度。两种流体通过混合元件（叶片）水平分裂，分裂的材料通过螺旋运动而变形，从而导致操作结束时条纹的数量增加。在下一个半期开始时，材料被垂直分割，并重复类似的操作（拉伸和堆叠）。对插入圆形通道中的混合元件的数量重复相同的操作。

混合分析

粒子跟踪方法用于分析混合。给定速度场，最初位于具有不同幂律指数n的两种流体之间的界面处的粒子被跟踪到混合器几何结构的末端。横截面积的分布越均匀，混合效果越好。粒子追踪的最终结果在示踪粒子的分布中是明显的。根据关于颗粒分布的信息来评估混合均匀性。混合的一个适当度量是颗粒分布的均匀性，例如任何横截面上颗粒的信息熵。沿着这些路线，混合过程的表征首先需要将混合器横截面分成多个单元。然后，对于特定的粒子配置，混合熵S被定义为构成横截面积的单个细胞的信息熵之和，定义为

图 11.2 Kenics混合器的工作原理由两种灰色表示流体颗粒混合物。

N是单元数，ni是第i个单元处的粒子数密度。我们使用归一化熵增加S*作为混合的度量，而不是在混合分析中直接使用信息熵

S0是入口处的熵，Smax是最大可能熵，由log N定义，这是粒子均匀分布的理想情况，即ni¼1/N。图11.3显示了以方程式（11.9）中定义的归一化熵增加为特征的混合过程。在该图中，指数n对混合过程的影响并不显著，但这是参数研究和设计过程的一个示例。

11.2 注塑成型过程的建模与模拟

用于塑料的模型和模拟已应用于PIM，但高固体含量通常会造成塑料模拟中忽略的差异。一些情况证明了这些问题，如焊缝处的粉末粘合剂分离、高惯性效应（如成型钨合金）以及快速热损失（如成型铜和氮化铝）。此外，粉末粘合剂混合物对剪切速率非常敏感。因此，计算机模拟支持从塑料中展示的成功构建成型，并将这些概念应用到新的定制PIM模拟中，用于填充、包装和冷却。

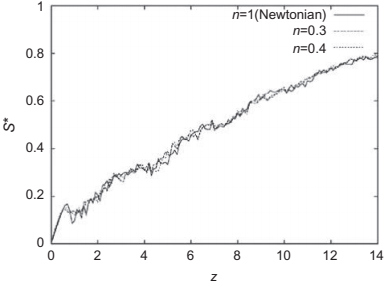
图 11.3 根据粘度模型中的指数n，以归一化熵为特征的混合过程沿轴向z增加S*。

11.2.1 理论背景和控制方程

典型的注塑部件的厚度比整体最大尺寸小得多。在模制这种部件时，熔融粉末粘合剂原料混合物是高粘度的。因此，雷诺数（表征惯性力与粘性力之比的无量纲数）远小于1，并且流动被建模为具有润滑的蠕动流动，如用Hele-Shaw公式处理的那样。利用Hele-Shaw模型，将注射模腔中熔体流动的连续性和动量方程合并为一个关于压力和流动性的泊松方程。由于薄壁和轴对称性，计算机模拟通常基于2.5维方法。但赫尔-肖模型有其局限性，无法准确描述熔体前沿的三维流动行为，称为喷泉流动，厚度突然变化的厚部件会出现特殊问题，从而导致赛道流动。目前，已有几种三维计算机辅助工程（CAE）模拟成功地预测了传统塑性推进和压力随部件设计和成形参数变化的情况。在本节中，我们将重点介绍2.5维方法，而不是全3D方法，因为2.5维方法更稳健，也更为业界所接受。

填充阶段

PIM涉及每隔几秒钟重复一次的循环。在循环开始时，成型机螺杆在桶中旋转并向后移动，以便在模具关闭时为下一个注射循环准备熔融原料。当往复螺杆向前移动时，模腔填充，起到柱塞的作用，这称为填充阶段。在填充阶段，使用连续介质方法建立控制方程系统，如下所示。

质量和动量守恒：在不可压缩流的假设下，质量守恒，也称为连续性方程，表示为

x、y和z是笛卡尔坐标，u、v和w是相应的正交速度分量。关于动量守恒，利用润滑和Hele-Shaw近似，对填充阶段熔融原料的Navier-Stokes方程进行如下修正：

P是压力，z是厚度，h是PIM原料的粘度。将等式（11.10）、（11.11）与z方向（厚度方向）的积分相结合，得出

其中

方程（11.12）是填充阶段的流量控制方程。这与通过将温度T代入P并将热导率k代入S而获得的稳态热传导方程完全相同。在这个类比中，S是流动性或流动性。作为对该流动控制方程的简单解释，熔融PIM原料从高压区流向低压区，流动速度取决于流动性S。

能量方程：根据填充阶段的润滑和Hele-Shaw近似，能量方程简化如下：

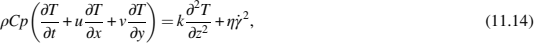
ρ是熔融PIM原料的密度，CP是熔融PIM原料的比热，γ=√(∂u/∂z)^2+(∂u/∂z)^2广义剪切速率，k是原料的热导率。

此外，我们需要一个本构关系来描述熔融PIM原料在腔填充期间对其流动环境的响应，这需要一个粘度模型。含有高浓度颗粒的聚合物有几种粘度模型可用。通常，它们包括温度、压力、固体负荷和剪切速率，本章稍后将介绍选定的模型。粘度模型的选择取决于加工条件范围内所需的模拟精度，例如温度和剪切速率，以及获得用于获得材料参数的实验程序的途径。

一旦我们有了基于连续体的守恒定律的微分方程组和用于填充阶段分析的本构关系，我们就需要边界条件。填充阶段的典型边界条件如下：

• 流动方程的边界条件：注入点的流速、熔体前沿的自由表面、空腔壁的无滑移条件；

• 能量方程的边界条件：注射点的注射温度、熔体前沿的自由表面、型腔壁的模壁温度条件。

请注意，唯一需要的初始条件是喷射节点处的流速和喷射温度，这是所需的边界条件之一。

包装阶段

当模具填充接近完成时，包装阶段开始。这促使注塑机的冲压控制策略发生变化，从速度控制变为压力控制，这被称为切换点。当空腔接近填充时，压力控制确保在闸门冻结之前填充空腔的填充和加压。重要的是要意识到填料压力用于补偿下一冷却阶段的预期收缩。原料体积收缩是由粘结剂的高热膨胀系数引起的，因此，冷却是可测量的收缩。闸门冻结前的填料压力过低会因部件收缩而产生下沉痕迹，而填料压力过高会导致喷射困难。因此，冷却前的适当增压对部件质量至关重要。对于填充阶段的分析，必须考虑熔体压缩性的影响。使用比体积对压力和温度的依赖性来考虑熔体的可压缩性，从而得出原料比压力-体积-温度（pvT）关系或状态方程。几种模型可用于描述PIM原料的PVT反应，如双域修正Tait模型和IKV模型。这些模型预测了用于粘合剂的半结晶聚合物的突然体积变化和用于粘合剂的非晶聚合物的较小突然体积变化。

在适当的粘度和pvT模型下，基于连续介质方法的填充阶段控制方程系统如下。

质量守恒：可压缩PIM原料的连续性方程表示为

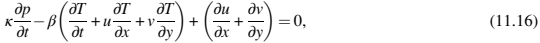
假设在填料阶段可以忽略压力对流项

κ是材料的等温压缩系数(∂ρ/ρ∂p） β测量材料的体积膨胀率(∂ρ/ρ∂T） （2）。这些很容易从状态方程中计算出来。注意，无论材料是否可压缩，都使用与等式（11.12）相同的动量守恒。

能量方程：能量方程导出为

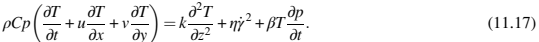
也就是说，出于实际目的，填料中可压缩情况的剪切速率与填充阶段的剪切速率相同。

填料阶段的典型初始和边界条件如下：

• 初始条件：来自填充阶段分析结果的压力、速度、温度和密度；

• 质量和动量守恒方程的边界条件：注入点的规定压力、熔体前沿的自由表面、空腔壁的无滑移条件；

• 能量方程的边界条件：注射点的注射温度、熔体前沿的自由表面以及与冷却阶段分析相联系的型腔壁的模具壁温度条件。

冷却阶段

在注塑过程的三个阶段中，冷却阶段显著影响最终部件的生产率和质量。注入原料熔体后立即开始冷却，但冷却时间通常指浇口冻结且不再有原料熔体进入模腔后的时间。当温度低到足以承受喷射应力时，它会持续到部件喷射点。在冷却阶段，原料体积收缩被压力衰减抵消，直到局部压力降至大气压。此后，材料随着任何进一步冷却而收缩，可能由于不均匀收缩或模具约束（在烧结之前可能无法检测到）而导致残余应力。在此阶段，由于冷却阶段原料熔体的速度几乎为零，因此忽略了能量方程中的对流和耗散项。因此，模具冷却分析的目的是仅求解型腔表面的温度分布，在填充和填充分析期间用作原料熔体的边界条件。当注射成型过程处于稳定状态时，由于热熔体和冷模具以及循环冷却剂之间的相互作用，模具温度将在过程中随时间周期性波动。为了减少该瞬态过程的计算时间，采用3D循环平均法进行热分析，以确定循环平均温度场及其对PIM组件的影响。尽管模具温度被假定为随时间变化不变，但PIM原料仍不敏感，导致以下特征。

模具冷却分析：在这种循环平均概念下，注塑模具冷却系统的传热控制方程如下

T是模具的循环平均温度。

PIM部件冷却分析：在不调用流场的情况下，能量方程简化为

冷却阶段应用的典型初始和边界条件如下：

• 初始条件：根据包装阶段分析计算的温度；

• 模具的边界条件：来自PIM原料冷却分析的界面输入、与冷却剂相关的对流热传递、与空气的自然对流热传递以及来自模具压板的热阻条件；

• 零部件的边界条件：来自模具冷却分析的界面输入。

注意，模具和PIM原料冷却的边界条件相互耦合。有关这一点的更多详情，请参见第11.2.2节的数值模拟。

11.2.2 数值模拟

就注塑成型的数值分析而言，已有几种数值包可用于传统热塑性塑料，人们可以尝试将相同的数值分析技术应用于PIM。然而，粉末粘合剂原料混合物的流变行为与热塑性塑料的流变行为明显不同。因此，将热塑性塑料开发的方法直接应用于PIM需要谨慎。商业软件包，包括Moldflow，Moldex 3D，PIMsolver和SIMUFLOW，可用于PIM模拟。这些商业软件包是基于其自身的技术和历史背景而开发的，这导致了其自身的利弊。此外，几个研究小组编写了定制代码，但通常不会发布供公众使用。

填充和包装分析

对于PIM的填充和填充阶段的数值分析，必须在整个填充和填充循环期间求解压力和能量方程。这是使用方程（11.11）的FEM实现的，而在z方向（厚度）上使用有限差分法（FDM），使用xy平面中的相同有限元来求解方程（11.12）。

FDM是求解微分方程的一种相对有效且简单的数值方法。在该方法中，物理域以有限差分网格的形式离散。生成一组代数方程作为偏微分方程的导数，这些方程由网格点处变量值的有限差表示。得到的代数方程组通常形成一个禁止矩阵，用数值方法求解。通常，通过减小网格间距来提高求解精度。然而，由于FDM很难应用于高度不规则的边界或注塑成型典型的复杂区域，因此该方法的使用必须限于规则和简单区域，或与FEM一起用作FDM-FEM混合方案。

对于PIM填充过程的数值分析，必须在整个填充循环中求解压力方程和能量方程，直到注射模腔被填充。采用有限元方法求解方程。（11.11），（11.12），而在厚度方向或z方向上使用FDM，在x-y平面上使用相同的有限元。

冷却分析

对于PIM中冷却过程的数值分析，边界元法（BEM）由于其在降低解的维数方面的优势而被广泛使用。边界元法离散了域边界，而不是物理域内部。因此，体积积分变为表面积分，然后未知数、计算工作量和网格生成显著减少。基于格林第二恒等式的等式（11.18）的标准边界元公式得出如下：

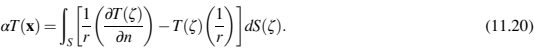
这里，x和z与模具中的位置向量r有关=丨z-x轴丨，a表示由边界表面形成的立体角。对于两个闭合曲面，如由部件形状定义的方程（11.18），导致最终线性代数方程组中的冗余，因此使用了一种修改的程序。对于圆孔，基于线下沉近似创建一个特殊公式。这种方法避免了圆形通道沿圆周的离散化，并显著节省了计算机内存和时间。对于PIM部件的热分析，FDM与Crack Nicholson算法一起用于时间推进。模具和PIM部件分析在边界条件下相互耦合，因此需要迭代直到解收敛。

填充、包装和冷却阶段之间的耦合分析

填充、包装和冷却的分析是相互耦合的。当我们分析填充和包装阶段时，我们将空腔壁温度作为能量方程的边界条件。这个腔壁温度是从冷却分析中得到的。另一方面，当我们分析冷却阶段时，我们将填充和包装结束时粉末-粘合剂原料混合物在厚度方向上的温度分布作为粉末-粘合剂原料传热的初始条件。这个初始温度分布是通过填充和包装分析得到的。因此，为了获得准确的数值模拟结果，可以对填充、包装和冷却阶段进行耦合分析。

PIM过程计算机模拟的典型程序包括三个部分：输入数据、分析和输出数据。输入数据的质量对成功至关重要。预处理器是一个软件工具，用于为部件和模具准备几何模型和网格；它包括原料、模具和冷却剂的材料数据，以及填充、包装和冷却过程的加工条件。图11.4显示了U形部件（包括输送系统和冷却通道）的几何建模和网格生成示例。

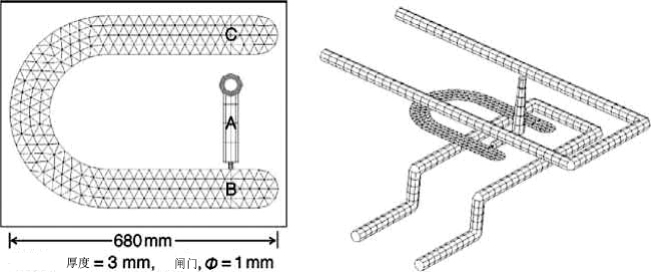
图11.4 U形零件的几何建模和网格生成，包括输送系统和冷却通道（A、B和C处的压力测量）

11.2.3 实验材料特性和验证

填充阶段的材料特性

PIM期间填充阶段的成功模拟取决于测量材料特性，包括密度、粘度和热行为。其中，PIM原料的粘度及其随温度、剪切速率和固体体积分数的变化尤其值得关注。以下步骤是用于获得这些材料特性的方法的示例。对于这个例子，假设在蜡聚合物粘合剂中有一个球形不锈钢粉末。

• 首先，需要原料的熔体密度、热容和热导率。这些是使用氦比重瓶、差示扫描量热计和激光闪光热导装置获得的。

• 其次，再次使用差示扫描量热法测量原料的转变温度。

• 第三，根据关键参数测量原料粘度。通过毛细管流变仪测量原料的流变行为。通过使用长径比高的毛细管，可以避免压力损失校正，即巴格利校正。提取Rabinowitch校正，以从非牛顿流体的表观剪切速率（原料特性）获得真实剪切速率。通过在高于转变温度的不同温度下测试原料来确定粘度随温度的变化。然后，使用基于等式的标准负载聚合物概念对原料粘度数据进行建模。(11.2), (11.3).

填料阶段的材料特性

为了模拟填充阶段，假设非等温条件下PIM原料的可压缩粘性熔体的Hele-Shaw流动。为此，采用双域修正Tait模型来描述原料的相行为（Chiang等人，1991）。膨胀计用于测量作为温度和其他变量的函数的尺寸变化，并通过曲线拟合提取结果。

图 11.5 给出一个基于以下双域改性泰特模型的pvT材料特性的例子，用于不锈钢原料的包装阶段模拟。对于固液相。

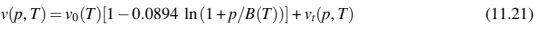
和

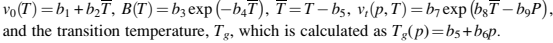
冷却阶段的材料特性

对于冷却阶段的模拟，需要测量模具材料和冷却剂的材料特性。

验证

仿真验证是任何基于仿真优化设计的努力之前的关键步骤。这种验证通常包括对软件开发中使用的模型的验证。为了通过实验证明模拟工具的验证，我们选择了图11.4所示的U形测试模具，其中使用了先前报告的不锈钢PIM原料和H13模具。使用三个压力传感器将模拟结果与实验数据进行比较。空腔厚度为3mm，浇口直径为1mm。冷却液入口温度为20°C，入口流速为50 cm3/s，冷却时间为10 s。

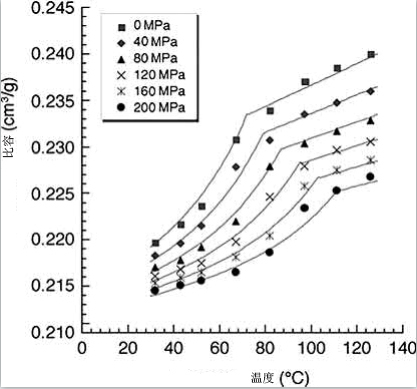
图 11.5 原料的压力-体积-温度（pvT）数据

图 11.6 描述了使用PIMsolver获得的一些模拟结果。图11.1A显示了填充模式，表明模具型腔是如何作为时间的函数填充的。填充时间为 1.28 秒。图板 11.1B 显示了冷却分析结果中模腔上下表面的平均温度分布，单位为 K。最高的平均温度是51°C，发生在U的底部，最低温度是34°C，在流道入口处。模壁温度并不均匀，最大值和最小值之间的差异为18℃。这种变化大到足以造成包装阶段凝固层发展的显著差异。因此，如果不考虑冷却效应，人们可能会认为模拟在包装阶段的压力预测上有很大的误差。

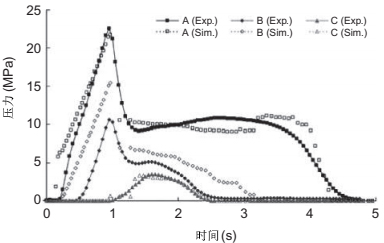
图 11.6 图11.4所示三个点的压力-时间图。

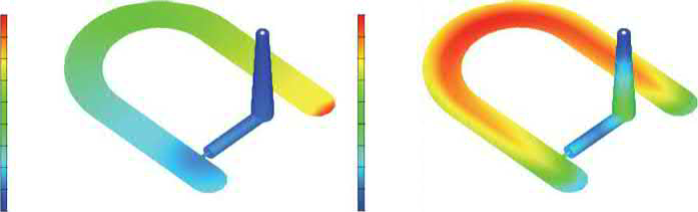
（A）                                                                    （B）

为了检验验证，如图11.6所示，使用图11.4所示的三个位置对模拟和实验之间的压力轨迹进行了比较。图11.6给出了从实验和模拟中获得的压力-时间曲线。模拟结果是在30℃的恒定腔壁温度下通过填充和填充分析获得的。如图11.6所示，模具壁温度分布的结果与冷却分析的结果相结合，解释了这种偏差。如果我们考虑冷却分析（耦合分析）中的空腔壁温度分布，则该温度能够与实验结果最佳一致。