MIM制模与模拟（11.3-11.5）

目录

• 11.3 热脱粘过程的建模与仿真

• 11.3.1 单个反应步骤的理论背景和控制方程MDC

• 11.3.2 应用

• 11.4 烧结过程的建模与仿真

• 11.4.1 理论背景和控制方程

• 11.4.2 材料性能的实验测定和模拟验证

• 11.4.3 应用

• 11.5 结论

11.3 热脱粘过程的建模与仿真

由于PIM是一种粘合剂辅助成型技术，因此在不损失产品完整性的情况下去除粘合剂是一个关键点。去除粘合剂的过程称为脱脂。多组分粘合剂可以通过在压实体中留下一个组分来将颗粒保持在适当位置，同时去除较低稳定性的组分来克服变形问题。通常，低分子量粘合剂组分在称为溶剂脱脂的过程中溶解到流体中。热脱脂是一种在气体气氛中进行的常规热处理，用于去除粘合剂体系中的高分子量组分。以前，脱脂循环基于“试错”，直到达到足够的时间-温度循环。使用多组分粘合剂系统时，在保持压实体形状的同时实现经济有效的脱脂循环可能相当困难。为了对抗这种情况，使用热重分析（TGA）和差热分析（DTA）来确定作为时间和温度的函数的粘合剂组分的剩余重量百分比。本协议旨在显示快速失重点的加热，以避免紧凑型损坏。这加快了脱脂过程并降低了总成本。但仍然需要大量的TGA和DTA实验来优化多组分粘合剂系统中各粘合剂组分的百分比。为了最小化TGA实验，提出了主分解曲线（MDC） 

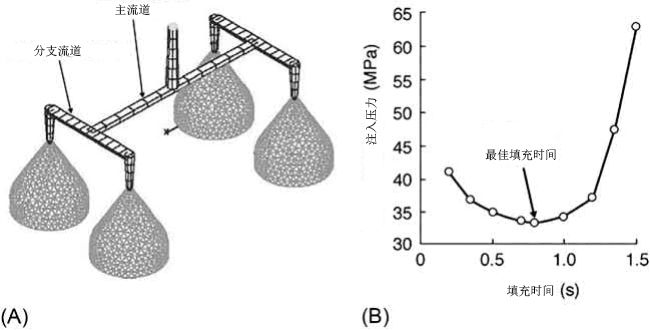
图11.7 使用CAE工具优化注塑成型的填充时间：（a）用于优化研究的网格；（B） 最大限度地减少注射压力的最佳填充时间发现

11.3.1 单个反应步骤的理论背景和控制方程MDC

聚合物粘合剂的解聚可以用一级反应动力学来描述。聚合物的剩余重量分数a表示为 

t是时间，K是热降解的速率常数，遵循阿伦纽斯方程

k0是比速率常数，Q是热降解的表观活化能，R是气体常数，T是绝对温度。结合公式（11.22）、（11.23），并进行积分

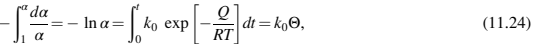
Q被称为分解功，定义如下：

聚合物的剩余重量分数α与方程式（11.24）中的分解功Q有关，如下所示：

前面提到的方程定义了MDC，其中我们可以使用分解功Q的概念将给定聚合物的分解曲线与任何分解循环合并。

表观活化能计算

为了计算分解功Q，需要根据等式（11.25）确定表观活化能Q。聚合物分解的活化能可以根据TGA数据确定。基辛格方法利用温度Tmax，在该温度下，在各种加热速率下出现最大失重率，如下所示：

以最大的减重速度

在恒定加热速率r的条件下，即dT/dT¼r，方程式（11.27）可以表示为

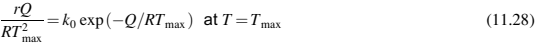
或

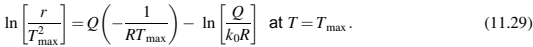
因此，根据等式（11.29），我们可以绘制出In[r/（Tmax）2]和1/RTmax之间的曲线图，该曲线图来自具有几个恒定加热速率的TGA实验。该曲线的斜率给出了反应的表观活化能Q。

多反应步骤的MDC

通常，聚合物降解的TGA曲线遵循单个S形路径。但由于不同聚合物组分的分子量、键合基团和降解路径不同，多组分粘合剂系统可能具有两个或多个乙状体。每个S形代表一个速率控制步骤，其活化能不同于其他控制步骤的活化能。为PIM量身定制的粉末粘合剂系统通常由几个部件组成。这些组分可根据其分子量主要分为两类。低分子量成分，如溶剂和增塑剂，在相当低的温度下蒸发或分解。高分子量聚合物具有较高的热稳定性，在相对较高的温度下分解。因此，TGA曲线通常有两个以上的S形曲线。这个曲线的一个S形可以是几个具有相似活化能的S形的叠加。该曲线的两个S形可以意味着两组具有足够分离的活化能的反应步骤。每个S形可以用阿伦尼乌斯型方程中的三个动力学参数来描述。这些参数是反应级数、活化能和频率因子。一些粉末可能对热解速率有催化作用；然而，有粉末的热解曲线的形状与没有粉末的相似。因此，聚合物热解的数学形式仍然可以应用。本研究中使用的粘合剂体系的两种聚合物在热脱粘过程中分解。

a是两种聚合物的初始质量的质量比，a1是低分子量聚合物的质量比与初始质量的比，a2是高分子量聚合物的重量比与初始重量的比，w是低分子聚合物的初始重量与两种聚合物初始质量的比值。

一般适用于聚合物的TGA曲线的数学形式被修改为描述有机热解粉末的TGA曲线。在本分析中，我们假设动力学完全由温度控制。

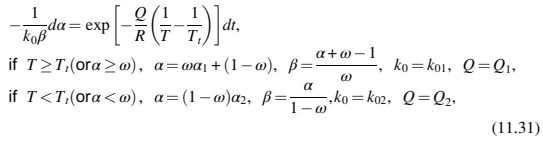
Tt是第一和第二S形曲线之间的转变温度，α、Q和k0上的下标1和2分别表示低温和高温降解。具有两个以上S形的分解动力学曲线可以用类似的方式表示。基辛格方法用于估算活化能，如前一节所述。

等式（11.31）的左侧仅为质量比α和材料特性的函数，Q除外，Q变为

等式（11.31）的右侧表示为

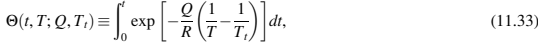
表格 11.1 粘合剂系统中使用的粘合剂组分的特性 

其仅取决于Q、Tt和时间温度分布。注F（a）是一个量化粘合剂系统组分对分解动力学的影响的特性。α和F（α）之间的关系被定义为MDC，它对于给定的粉末和粘合剂系统是唯一的，并且与分解路径无关，如前面所述的假设。

11.3.2 应用

活化能计算

表11.1列出了PIM中使用的蜡聚合物粘合剂的典型示例，并对每个粘合剂组分进行了表征。TGA是一种质量变化方法，其中在样品经受受控温度程序时，样品的质量作为温度的函数进行测量。这可以作为温度升高的函数或在受控气氛下等温作为时间的函数来实现。用三种不同加热速率下的每个粘合剂组分的结果进行TGA，以通过基辛格法计算活化能。然后将该活化能用于开发MDC。

图11.8A显示了三种不同加热速率下聚丙烯的TGA。很明显，分解范围为350-490℃。图11.8B给出了峰值 聚丙烯最大失重时的温度。将这些数据插入等式（11.29），绘制In[r/（Tmax）2]和-1/RTmax之间的曲线图（图11.8C）。该图的斜率给出了聚丙烯的表观活化能。表11.1给出了用于绘制MDC的每个粘合剂组件的材料参数。

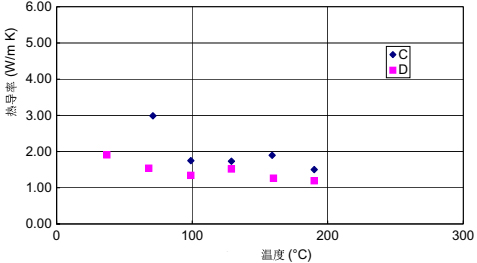
图11.8 TGA结果和基辛格法计算聚丙烯的活化能。（A） TGA结果。（B） 最大失重速率下的温度。（C） 温度依赖性。

用于单反应步骤分解的MDC

然后用公式（11.31）-（11.33）来绘制聚丙烯的MDC（图11.9）。聚丙烯在所有的加热速率下都表现出类似的分解行为。同样，其他粘合剂成分（石蜡、聚乙烯和硬脂酸）的MDC是根据其各自的TGAs（此处未显示），按照基辛格方法计算的活化能生成的。粘结剂系统的整体MDC是由其各个组分的MDC绘制而成的。粘结剂组分的单个分解行为在基本理解中很重要，但整个粘结剂系统的分解行为在PIM中更有意义。图11.10所示为粘结剂系统的这种行为。也可以看出，该模型与实验结果接近一致。此外，在任何时间-温度组合下，基于构建的MSCs，每个粘结剂成分的剩余重量可以被预测和监测。

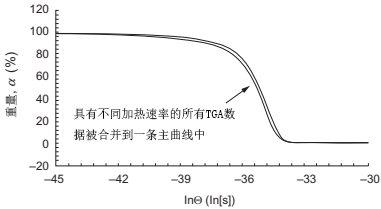
图 11.9 聚丙烯的MDC，显示所有TGA。

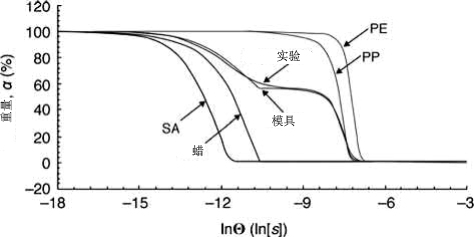
图 11.10 粘合剂体系整体分解行为的合成

用于多反应步骤分解的MDC

在决定注塑件的脱脂周期时，热脱脂过程中原料的分解行为至关重要。这使得原料的MDC在成本和工作量优化方面都是一个有吸引力的工具。为了证明这一概念并找出脱脂的工艺参数，使用铌原料（57%固体负载）。图11.11显示了铌原料MDC。观察到两步分解行为，其中在第一步期间，低分子量粘合剂组分（蜡和硬脂酸）分解，随后高分子量粘合剂组份（聚丙烯和聚乙烯）消失。还观察到，分解是速率依赖的，即在特定温度下，更多的粘合剂以更高的加热速率保持。对于纯粘合剂，情况并非如此。粉末对分解行为有影响。

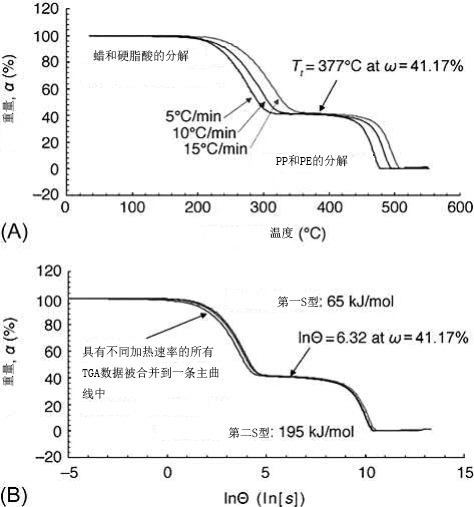
图 11.11 Nb原料的多反应步骤MDC（A） 原料1的TGA（B）原料1的MDC

金属粉末的影响

图11.12显示了纯粘结剂（D-binder）、Nb原料（D-Nb）和316L不锈钢原料（D-316L）的溶剂剥离样品的MDC。可以观察到，对于特定的粘合剂wt%，原料（D-Nb和D-316L）需要比没有任何粉末的粘合剂更低的温度（这里更高的分解功Q）。这似乎是合理的，因为粉末的存在将增强脱粘过程，并且将需要更高的分解功（更低的温度），这是由于金属粉末的更高导热率（Nb为54W/m K，316L为12W/m K；而典型聚合物为0.1W/m K）而产生的催化效应或更快的热传递。还可以考虑D-Nb和D-316L的MDC之间的另一差异。这也可以解释粉末形状对脱脂过程的影响。D-Nb是具有不规则形状的Nb颗粒的铌原料，而D-316L是具有球形粉末颗粒的316L原料。两种原料具有相同的固体负载（57体积%）。与不规则形状的粉末相比，球形粉末颗粒具有较低的表面积。从MDC（图11.12）也可以明显看出，与D-316L（球形）相比，D-Nb（不规则）脱脂所需的分解功更低。最后，得出的结论是，催化剂、导热系数和颗粒形状效应共同作用于粘合剂与金属粉末的分解行为。需要进行详细分析，以便更准确地解释。

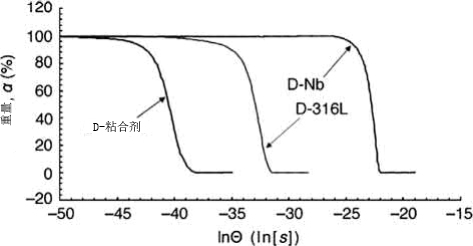
图 11.12 金属粉末对分解行为的催化作用图解

重量-温度-时间图

图11.13显示了在氢气气氛中溶剂脱粘316L原料分解的重量-温度-时间图。基于此信息，可以预测给定温度和目标粘合剂重量损失所需的保持时间。这将有助于减少确定最佳脱脂周期所需的实验。

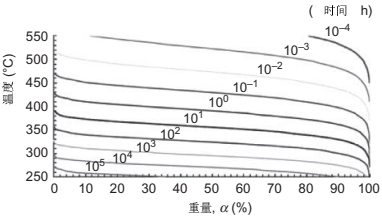
图 11.13 溶剂脱粘316L原料分解的重量-温度-时间图 

11.4 烧结过程的建模与仿真

有效的计算机模拟金属粉末烧结是粉末冶金行业的愿望之首。由于压制的坯体不均匀，因此需要采用落后的解决方案来选择粉末、混合、注射成型、脱脂和烧结属性，以在不同的工具设计、机器和加工条件下实现目标性能。为了实现这一目标，对各种模拟类型进行了评估：蒙特卡罗、有限差分、离散元、有限元、流体力学、连续介质力学、神经网络和自适应学习。不幸的是，输入数据和一些基本关系没有得到很好的发展；在相关条件下，大多数材料缺少准确的数据。模拟有助于定义处理窗口并设置初始操作参数。

11.4.1 理论背景和控制方程

用于模拟烧结的方法包括连续体、微观力学、多粒子和分子动力学方法。它们的长度尺度不同。在这些方法中，连续体模型具有计算时间最短的优点，能够预测相关属性，如成分密度、粒度和形状。

烧结过程中的本构关系

连续建模是模拟烧结过程中晶粒生长、致密化和变形的最相关方法。基于烧结机制，如表面扩散、晶界扩散、体积扩散、粘性流动（对于非晶材料）、塑性流动（对于结晶材料）、蒸发冷凝和重排。对于工业应用，现象学模型用于烧结模拟，具有以下关键物理参数。

• 烧结应力是由于孔隙和晶界的界面能而产生的烧结驱动力。烧结应力取决于材料的表面能、密度和几何参数，如在最后阶段关闭所有孔隙时的粒度。

• 有效体积粘度是烧结过程中致密化的阻力，是材料、孔隙率、粒度和温度的函数。根据假定的主要烧结机理，有效体积粘度的模型有多种形式。

• 有效剪切粘度是烧结过程中对变形的阻力，也是材料、孔隙率、粒度和温度的函数。有效体积粘度的几种流变模型是可用的。

前面提到的参数是粒度的函数。因此，需要一个晶粒生长模型来准确预测烧结过程中的致密化和变形。

烧结模拟的典型初始和边界条件包括：

• 初始条件：从压实模拟中获得的用于晶粒生长的生坯的平均粒径和晶粒尺寸以及用于致密化的初始生坯密度分布；

• 边界条件：施加在自由表面上的表面能条件和部件的摩擦条件，取决于其尺寸、形状和与支撑基板的接触。

压制体内的初始生坯密度分布提高了用精确压实模拟的输出开始烧结模拟的必要性，因为模具压实会产生取决于材料、压力、加压速率、工具运动和润滑的生坯密度梯度。初始和边界条件有助于确定烧结过程中因重力、非均匀加热和坯体密度梯度而产生的形状变形。

数值模拟

尽管已经开发了许多数值方法，但有限元法最适用于压力机和烧结过程的连续模型。FEM方法是一种数值计算方法，通过应用于每个元素的近似函数来求解微分方程组，称为逐域近似。这种方法对于粉末冶金中遇到的典型复杂几何形状非常有效。这是最早应用于材料建模的技术之一，目前在整个行业中都在使用。许多强大的商业软件包可用于计算2D和3D热机械过程，如烧结过程中发现的那些过程。为了提高烧结模拟的精度和收敛速度，模拟工具的开发人员已经选择了用于时间推进的显式和隐式算法，以及用于诸如表面分离等问题的数值接触算法，以及如在一些烧结材料中看到的大变形所需的重网格算法，其中高达25%的尺寸收缩是可能的。

11.4.2 材料性能的实验测定和模拟验证

在开发烧结模拟的本构模型时，需要进行各种各样的试验，包括晶粒生长、致密化（或膨胀）和变形的数据。这些方法如下。

• 晶粒生长：从加热循环中的不同点进行淬火试验，并分析安装的横截面，以获得晶粒尺寸数据，从而实现晶粒生长模型。使用立式淬火炉将压块烧结到烧结循环中的各个点，然后在水中淬火这些压块。这给出了密度、化学溶解（例如，一种成分向另一种成分的扩散）和粒度作为温度和时间的瞬时函数。在光学或扫描电子显微镜（SEM）之前，对淬火样品进行切片、安装和抛光。如今，自动定量图像分析提供了密度、晶粒尺寸和相含量相对于压坯位置的快速测定。通常在烧结期间，平均晶粒尺寸G与初始平均晶粒尺寸G0（在生坯上确定）不同。应用新的主烧结曲线概念，将实验粒度数据拟合到烧结的整体工作中，因为实际循环是加热和保持的复杂组合。所得材料参数可追溯到表观活化能作为唯一可调参数。图11.14显示了液相烧结（LPS）期间W-8.4wt%Ni-3.6wt%Fe混合粉末压坯的淬火试验和晶粒生长模型后的SEM显微照片。

• 致密化：为了获得致密化所需的材料参数，使用恒定加热速率膨胀法原位测量收缩率、收缩率和温度。通过将实验数据拟合到包括烧结应力σs和体积粘度K作为密度和粒度函数的模型，再次依赖于主烧结曲线概念，提取了少数未知材料参数。图11.15显示了用于获得316L不锈钢烧结过程中参数的膨胀测量数据和模型曲线拟合结果。

• 变形：粉末冶金压块在烧结过程中达到非常低的强度水平。因此，重力、基底摩擦和不均匀加热等弱力将导致变形甚至开裂。为了获得与变形相关的材料参数，使用三点弯曲或烧结锻造实验对变形进行原位测量。通过将实验数据与剪切粘度M与晶粒生长的有限元模拟进行拟合，提取了表观活化能和参考剪切粘度等参数。图11.16显示了现场弯曲试验和FEM结果，用于获得掺有0.2%硼的316L不锈钢粉末的剪切粘度的材料参数，以诱导改善的烧结。

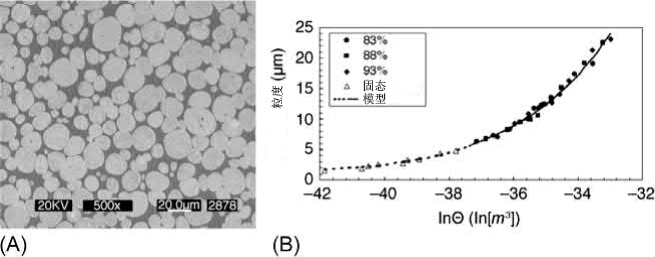
图 11.14 （A） 淬火后液相烧结钨重合金的SEM。（B） 粒度模型取自烧结概念的整体工作

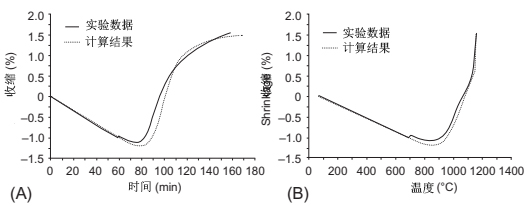
图 11.15 显示恒定加热速率实验期间原位收缩数据的膨胀测量数据和用于获得

图 11.16 （A） 掺杂有0.2重量%硼的316L不锈钢样品在原位弯曲试验期间拍摄的视频图像。（B） FEM模型结果用于验证加热过程中剪切粘度特性随时间、温度、粒度和密度的变化。

这样的数据提取技术已经应用于多种材料，包括钨合金、钼、氧化锆、硬质合金、铌、钢、不锈钢和氧化铝。表11.2是用作烧结模拟输入数据的W-8.4 wt%Ni-3.6 wt%Fe的材料特性示例集。上述实验技术可用于烧结模拟结果的验证。

11.4.3 应用

烧结过程中的重力畸变

烧结系统的流变数据允许系统响应驱动致密化的内部烧结应力和驱动变形的任何外部应力，例如重力。当压块烧结到高密度时，还需要诱导低强度（材料被热软化到内部烧结应力可以诱导致密化的点）。图11.17显示了一种钨重合金的烧结模拟结果，该结果依赖于在地球和微重力条件下获取的测试数据，然后预测地球、月球、火星和太空中各种重力条件下的预期形状。结果表明，重力会影响烧结过程中的形状变形。因此，计算机模拟可用于对生坯部件几何形状进行逆向工程，以预测变形，从而实现所需的烧结零件设计。

(A)                                                                         (B)

图 11.17 对于复杂的测试几何形状，在各种重力环境下烧结导致最终变形（A）T形（B）接头零件

烧结优化

通常，对于给定的烧结密度，需要小的粒度来改善性能。在本图中，设计变量是烧结循环。为了获得最大密度和最小晶粒度，建议使用以下目标函数F

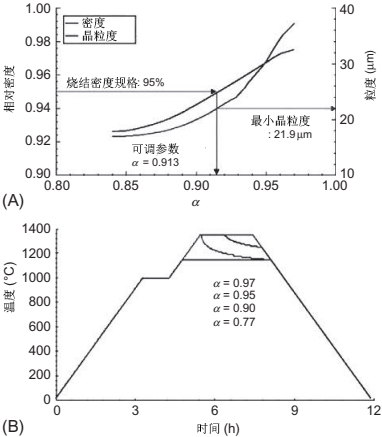
图 11.18 在17-4PH不锈钢中，给定最终烧结密度的最小晶粒尺寸和实现该目标的相应烧结循环（A）烧结密度和最小晶粒度。（B）烧结循环

a是可调参数。图11.18显示了17-4-PH不锈钢粉末的最大密度和最小粒度示例。例如，如果规定的烧结密度为95%或理论值，则最小晶粒尺寸为21.9μm。图11.18B通过匹配可调参数a的值显示了相应的烧结循环。

11.5 结论

PIM的计算机模拟已经取得了长足的进步，与标准有限元技术相结合，显示了指导工艺设置的巨大能力。此处所示为执行流程优化所需的PIM概念。尽管这些模型只是对现实的近似，但它们仍然有助于仔细检查对PIM过程的理解。在这方面，建模的最大价值在于过程知识的强制组织。在广泛实施方面仍存在若干障碍。最大的问题是，传统粉末冶金在很大程度上依赖于自适应过程控制，因为许多导致尺寸或质量变化的重要因素都没有被测量。颗粒尺寸、成分、工具磨损、熔炉位置的变化以及其他因素（如加热过程中颗粒之间的反应）都会影响PIM的重要尺寸控制方面，尽管标称性能（如强度、硬度或疲劳寿命）主要取决于平均组分密度。在这方面，特别是在初始过程设置方面，计算机模拟具有重要价值。然而，尺寸公差、内部裂纹或其他缺陷等重要属性超出了现有模拟的成本效益能力。此外，大量的材料、工艺、工具材料、烧结炉和工艺循环使其难以概括；需要大量的数据收集，才能达到模拟的临界点。因此，需要进行更多的研究和培训，才能将模拟转化为在实践中广泛应用的模式。即使如此，商业软件仍然可用，并且在初始过程定义中显示出巨大的价值，以建立新的组件。